Home

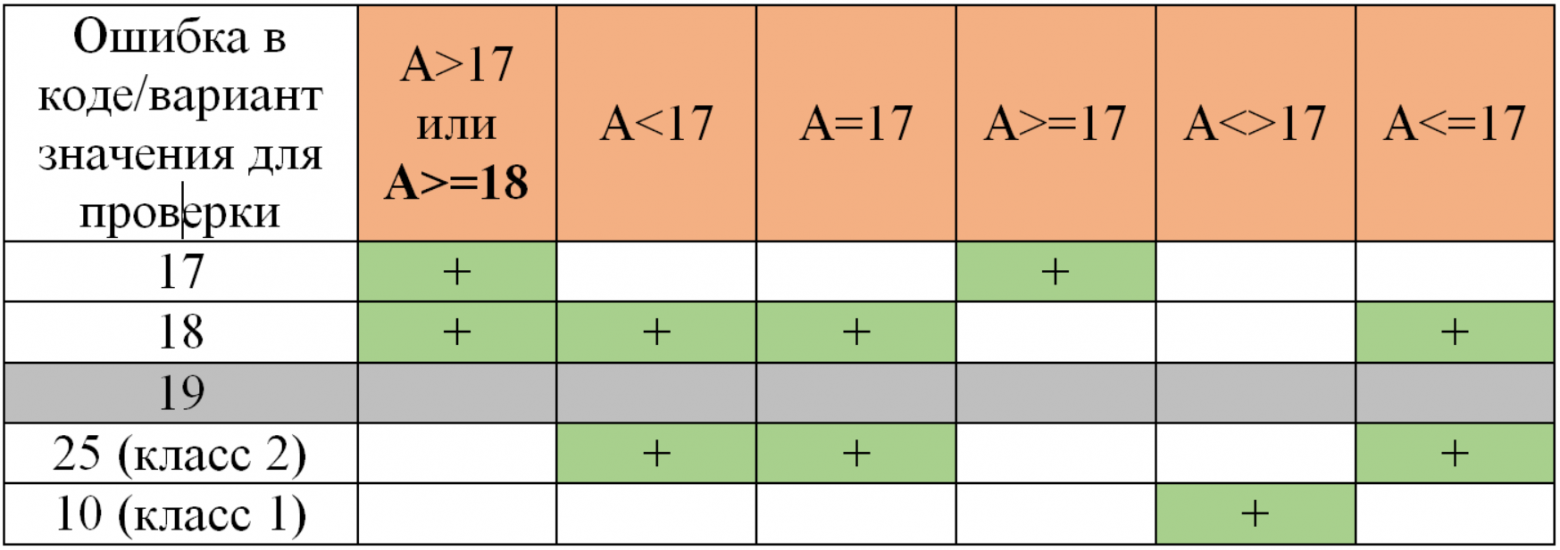
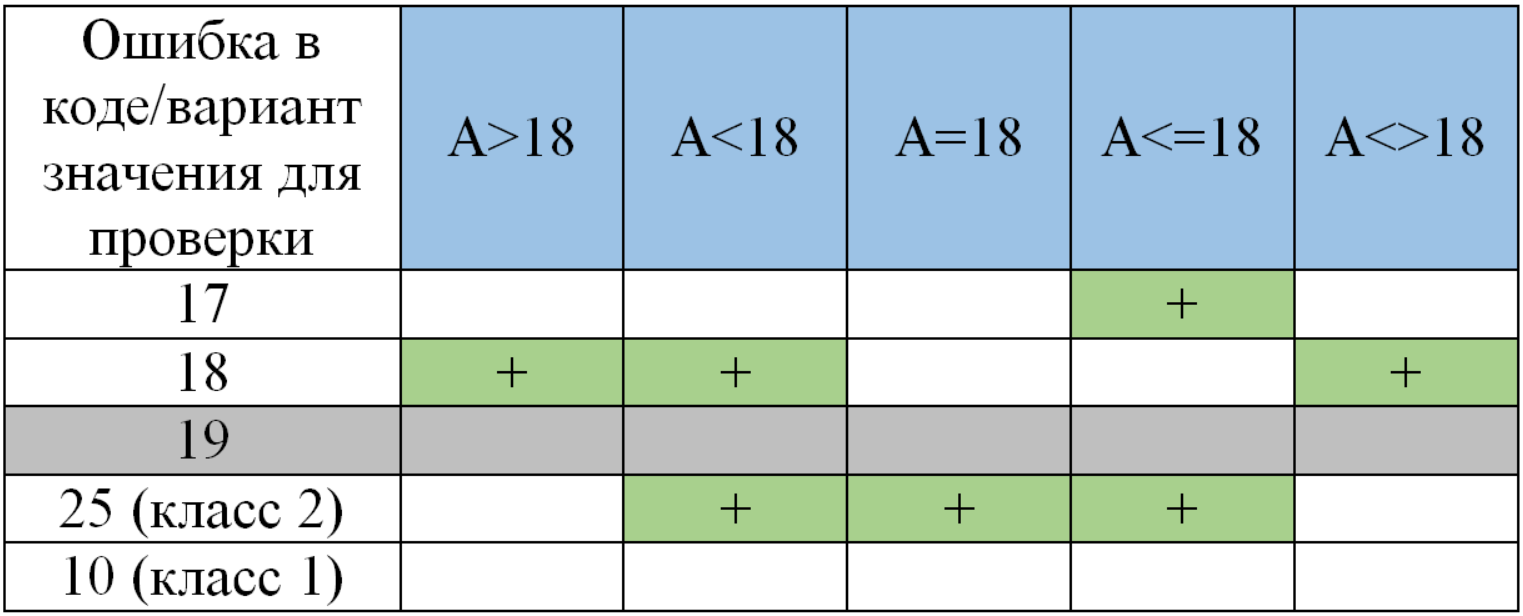
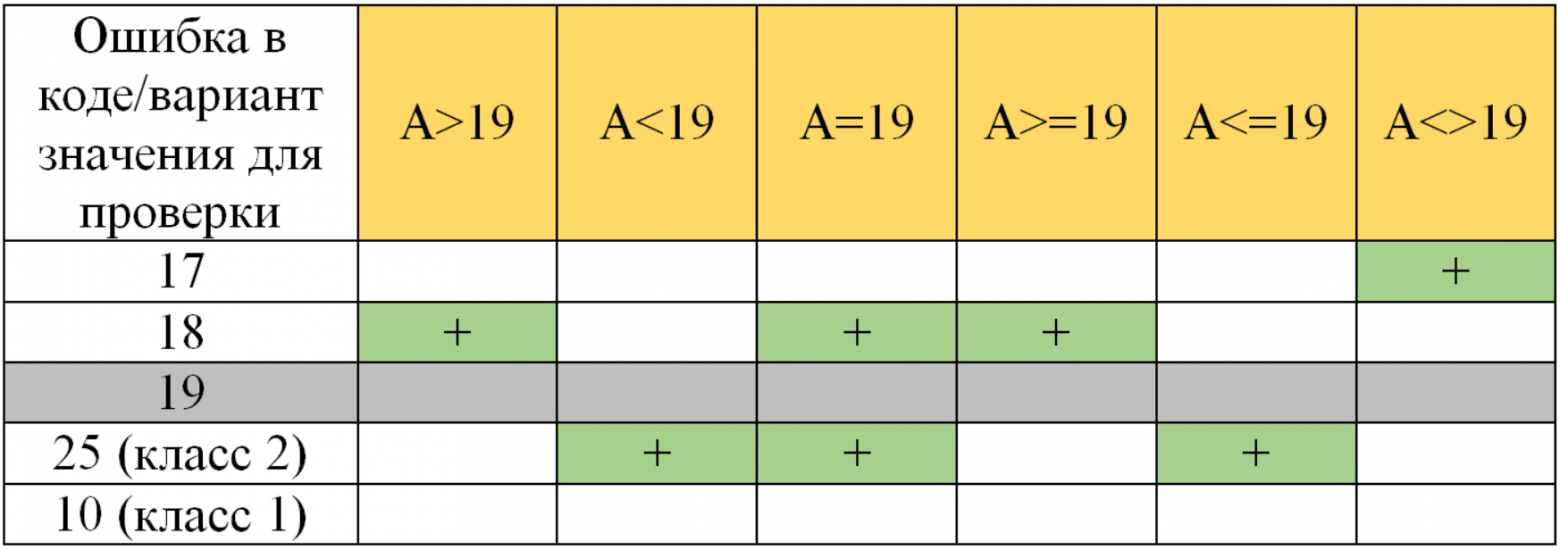
Автор: Смирнов Дмитрий

Оригинальная публикация

Большинство тестировщиков знакомы с такими техниками тест-дизайна, как разбиение на эквивалентные классы и анализ граничных значений.

Эти две техники, как и другие, призваны и позволяют значительно уменьшить количество необходимых проверок при тестировании, например полей ввода.

В двух словах напомню.

Эквивалентный класс – подмножество всех входных значений, которые будут обработаны приложением одинаково (из-за внутренней логики приложения), и на выходе дадут одинаковый результат. Собственно техника заключается в том, что достаточно проверить одного представителя класса вместо всех. Рекомендуется брать значение из середины класса, т.к. при этом ничто не влияет на логику обработки.

Граничные значения – значения диапазона входных данных, при которых меняется поведение приложения. Это соседние значения диапазона, но относящиеся к разным эквивалентным классам. И хотя сами граничные значения являются элементами/представителями своих классов, они должны быть протестированы в дополнение к проверке значения из середины класса. Почему? Необходимость заложена из предпосылок, что при написании кода, разработчик может ошибиться при указании границ и/или логики.

Перейдем к рассмотрению конкретного примера и оценки количества необходимых тест-кейсов.

Вопрос: сколько тест кейсов необходимо для покрытия граничных значений и классов эквивалентности на примере доступа к функционалу приложения на основе возраста (для целочисленных значений от 1 до 100)?

Здесь будут рассмотрены только позитивные сценарии без проверки границ диапазона 1 и 100 (без тестирования 0, отрицательных чисел, букв, спец. символов).

ТЗ: доступ к контенту разрешен только с 18 лет (т.е. возраст >= 18 лет).

Определим эквивалентные классы: 1-17 | 18-100 (1-17 – класс 1; 18-100 – класс 2).

Граничные значения: 17 и 18.

Классически тестируются два значения для границы (17 и 18 для нашего примера), когда при переходе от одного к другому меняется поведение (выходной результат). При этом граница не является конкретным значением, она определена граничными значениями двух соседних классов эквивалентности.

Значение 18 является элементом класса 18-100, и логически, если проверка проходит на 18, то нет никакой вероятности (кроме умышленного исключения значения 19 в коде), что 19 не пройдет проверку, т.к. оно является элементом того же класса 18-100.

То же самое справедливо для значения 17, если мы рассматриваем класс 1-17, нет никакой необходимости тестировать значение 16.

Встречается мнение о необходимости тестирования границы с двух сторон, при этом граница определяется как конкретное значение, указанное в ТЗ (или первое, граничное значение класса). Этот подход либо не объясняется вообще (давайте на всякий случай протестируем +/- "границу"), либо тем, что программист может ошибиться в выборе границы и указать 17 (или 19) вместо 18.

И в дальнейшем предлагается тестировать три значения: 17 – нижняя граница, 18 – собственно граница, 19 – верхняя граница.

Составим некое подобие матрицы трассируемости/прослеживаемости (traceability matrix) для анализа покрытия случайных ошибок в коде нашими выбранными значениями.

Смоделированы следующие ошибки в коде: неверное определение границ (соседние числа к «границе» значений) и/или неверная логика (вариации со знаками неравенств).

В самих таблицах:

+ - значение покрывает тестируемую ситуацию (ошибку в коде).

Если вводим значение в пределах класса, и результат FALSE (должен, а не пускает) – у нас выявлена ошибка в коде.

Если вводим значение за пределами класса, и результат TRUE (не должен, а пускает) – у нас выявлена ошибка в коде.

А>=18 эквивалентно A>17 с точки зрения классов и их значений.

Вывод: из таблиц видно, что тестирование значений, не являющихся граничными (19) возможно, но оно бессмысленно (лишние тест кейсы), т.к. не является уникальным для покрытия каких-либо случайных ошибок в коде.

Ответ на поставленный ранее вопрос: 2 тест-кейса на каждую границу + 1 на каждый класс (для нашего примера проверяем значения 10, 17, 18, 25).

Обсудить в форуме