Что пишут в блогах
- Хочешь ещё быстрее?
- Мы незаметно перескочили странную границу
- Книга «SQL. Курс молодого бойца» уже в продаже!
- Перестать лайкать лайки
- Питер Сенге. Пятая дисциплина. Искусство и практика обучающейся организации
- Итоги 2025 года (родилась дочка, конференции, курс по ChatGPT)
- ChatGPT, подсчитай количество страниц в книге и авторских листов
- Вайб-кодинг и вайб-тестинг — полный гайд на реальных проектах в Cursor и ChatGPT
- Новогодний QA квиз
- Не просри свое время
Что пишут в блогах (EN)
- The Code You Can’t Delete
- AI and Testing: Personal Marketability
- Writing a recommendation
- Everyone is NOT Responsible for Quality
- My LinkedIn break - six weeks in
- AI and Testing: Scaling Tests
- When you outsource testing to the AI, you lose the ability to understand your system
- User Error (Update)
- The Box and The Arrow.
- Contraption.AI
Онлайн-тренинги
-
Автоматизация тестирования REST API на PythonНачало: 25 февраля 2026
-
Тестирование мобильных приложений 2.0Начало: 25 февраля 2026
-
Автоматизация тестирования REST API на JavaНачало: 25 февраля 2026
-
Тестирование безопасностиНачало: 25 февраля 2026
-
Python для начинающихНачало: 26 февраля 2026
-
Азбука ITНачало: 26 февраля 2026
-
Автоматизация тестов для REST API при помощи PostmanНачало: 26 февраля 2026
-
Применение ChatGPT в тестированииНачало: 26 февраля 2026
-
Школа для начинающих тестировщиковНачало: 26 февраля 2026
-
Практикум по тест-дизайну 2.0Начало: 27 февраля 2026
-
Тестирование производительности: JMeter 5Начало: 27 февраля 2026
-
Тестирование REST APIНачало: 2 марта 2026
-
Инженер по тестированию программного обеспеченияНачало: 5 марта 2026
-
Программирование на Java для тестировщиковНачало: 6 марта 2026
-
Организация автоматизированного тестированияНачало: 6 марта 2026
-
Тестирование без требований: выявление и восстановление информации о продуктеНачало: 9 марта 2026
-
Школа тест-менеджеров v. 2.0Начало: 11 марта 2026
-
Git: инструменты тестировщикаНачало: 12 марта 2026
-
Регулярные выражения в тестированииНачало: 12 марта 2026
-
Bash: инструменты тестировщикаНачало: 12 марта 2026
-
SQL: Инструменты тестировщикаНачало: 12 марта 2026
-
Docker: инструменты тестировщикаНачало: 12 марта 2026
-
Chrome DevTools: Инструменты тестировщикаНачало: 12 марта 2026
-
Автоматизация функционального тестированияНачало: 13 марта 2026
-
Логи как инструмент тестировщикаНачало: 16 марта 2026
-
Техники локализации плавающих дефектовНачало: 16 марта 2026
-
Тестировщик ПО: интенсивный курс (ПОИНТ) со стажировкойНачало: 17 марта 2026
-
Школа Тест-АналитикаНачало: 18 марта 2026
-
Charles Proxy как инструмент тестировщикаНачало: 19 марта 2026
-
Создание и управление командой тестированияНачало: 19 марта 2026
-
CSS и Xpath: инструменты тестировщикаНачало: 19 марта 2026
-
Тестирование GraphQL APIНачало: 19 марта 2026
-
Тестирование веб-приложений 2.0Начало: 20 марта 2026
-
Программирование на C# для тестировщиковНачало: 27 марта 2026
-
Selenium IDE 3: стартовый уровеньНачало: 3 апреля 2026
-
Аудит и оптимизация QA-процессовНачало: 3 апреля 2026
-
Программирование на Python для тестировщиковНачало: 3 апреля 2026
| Классы эквивалентности для строки, которая обозначает число |
| 02.02.2011 18:28 |
|
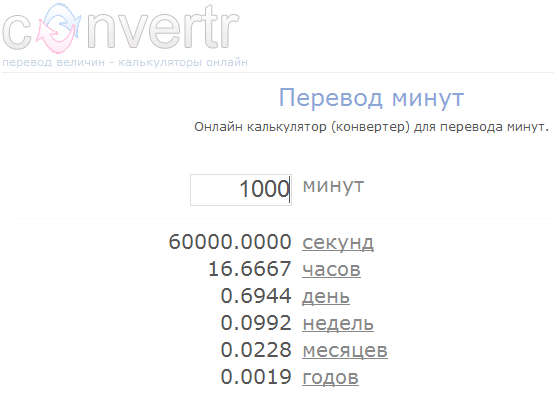
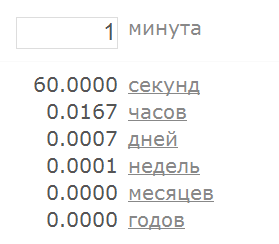
Автор: Алексей Баранцев Ещё в самом начале предыдущего онлайн-тренинга "Практикум по тест-дизайну" я обещал ученикам написать о том, как выполнять разбиение входных данных на подобласти (классы эквивалетности) в ситуациях, когда в поле ввода можно указать произвольную строку, а по смыслу туда должно быть введено число. Увы, им пришлось выполнять домашние задания без моих подсказок (впрочем, может быть это совсем не плохо). Но я всё таки решил перед тем, как начнутся занятия следующей группы, написать небольшую “шпаргалку”. Подавляющее большинство книг и статей, где описывается эта техника, в качестве примера рассматривают разбиение на классы множества чисел. При этом совершенно не учитывается тот факт, что в реальных приложениях с пользовательским интерфейсом все поля ввода строковые, и даже если есть ограничения на вводимые символы – это тоже предмет тестирования. А что рекомендуется делать с “нечислами”? Они все объединяются в один большой класс “невалидных” данных, из него наугад берётся одно-два значения и всё. И всё? А вот и нет! Представление о том, что из себя представляет “число” сильно зависит от конкретной реализации, и я покажу вам распространённые примеры строк, которые с точки зрения программы являются числом, хотя не всякий об этом догадается. А также опишу общую схему рассуждений, позволяющую выполнить разбиение на классы эквивалетности для строковых полей ввода, предназначенных для ввода числовых значений. Итак, давайте представим себе, что у нас есть приложение, которое на вход принимает строку, но по смыслу она должна интерпретироваться как число. Например, вот такое: Онлайн-калькулятор для перевода единиц времени.
Все возможные строки, разумеется, можно разделить на два больших класса – “числа” и “нечисла”. Но я дам этим классам другие, более длинные, но при этом более точные названия:
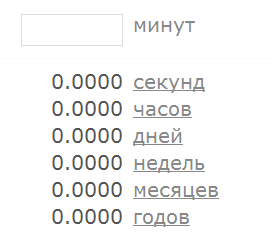
В такой формулировке сразу становится ясно, что программа на вход получает строку, которая перво-наперво по каким-то правилам преобразуется в число. Если это преобразование прошло успешно – полученное число используется в вычислениях, результат которых мы можем наблюдать. А если преобразовать строку в число не удалось – мы получаем информацию об этом либо в виде сообщения о возникшей проблеме, либо в виде “бессмысленного” результата вычислений. Мы можем без труда определить, как именно наш преобразователь времени ведёт себя в той и в другой ситуации, для этого достаточно подать на вход какое-нибудь значение, которое вне всяких сомнений должно интерпретироваться как число (например, “1”):
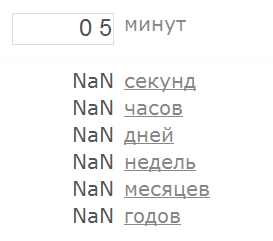
а также какое-нибудь значение, которое абсолютно точно числом не является (например, “привет”):
То есть здесь мы как раз имеем случай, когда “невалидное” входное значение приводить к бессмысленному результату (NaN означает “Not a Number”). Теперь давайте попробуем определить, какие же строки программа будет интерпретировать как числа, то есть начнём выделять в наших больших классах подклассы меньшего размера, но зато описанные конструктивно. Начнём с простого: 1.1. строка, представляющая собой последовательность цифр, интерпретируется как целое число. Очевидно? Вполне. Хотя нет, не совсем очевидно. Наверняка вы уже готовы были поймать меня за руку – какой длины последовательность цифр интерпретируется как число? Всё верно, правильный вопрос. Чтобы ответить на него, нужно опять применить технику разбиения на подобласти. Впрочем, здесь мы как раз имеем достаточно простой случай – длина последовательности это целое неотрицательное число, так что техника работает в полном соответствии с учебниками. Минимальная длина последовательности – ноль. Максимальная длина – “сколько влезет”. А сколько влезет? И куда влезет? В обсуждаемом приложении не указано никаких ограничений на размер поля ввода. Может быть браузер накладывает какое-нибудь ограничение, но лично мне про это ничего не известно, и даже если оно есть – наверняка в разных браузерах оно разное. Если введённые данные передаются на сервер в виде GET-запроса, возможно, имеется ограничение на длину запроса – согласно стандарту RFC 2068 они должны поддерживать не менее 255 байтов, но конечно же все реально способны обрабатывать запросы большей длины, и конечно же это опять зависит от браузера и от веб-сервера. Конвертер, который мы используем в качестве примера, реализован на языке JavaScript, на сервер никаких данных не отправляется, все вычисления производятся внутри браузера. Установленный на моём ноутбуке Google Chrome успешно справился со строкой, состоящей из 10 000 000 девяток, а вот строку из 100 000 000 девяток он обработать уже не смог – после длительного раздумья он вывел сообщение “Опаньки…” и предложил перегрузить страницу, потому что на ней возникла ошибка. Следовательно, где-то между этими значениями и находится та самая максимальная длина, определяемая по принципу “сколько влезет”. Поэтому уточняем: 1.1. строка, представляющая собой последовательность цифр, интерпретируется как целое число, если длина строки не превышает некоторое Максимальное Значение. Впрочем, куда раньше, на существенно более коротких последовательностях, начинает наблюдаться вот такая картина (скриншот показывает ситуацию, когда введена последовательность из 1000 девяток):
При вычислениях возникло переполнение, однако Infinity – это не NaN, то есть согласно описанном выше уговору мы будем считать, что такая последовательность (а также и более длинные последовательности цифр) всё таки может считаться числом. А что там с другой стороны? Последовательность нулевой длины – это пустая строка. Число ли это? Чуства и логика подсказывают, что нет, однако приложение не согласно с ними и интерпретирует пустую строку как число ноль:
На всякий случай ещё проверим последовательности длины 1, как ближайшей к минимальной граничной. Только чур не пытайтесь найти такую длину, при которой ещё не происходит переполнения, потому что это уже к длине не имеет никакого отношения, здесь важна уже не длина последовательности цифр, а само значение числа. Это оставим читателю в качестве упражнения (подсказка: JavaScript реализует стандарт IEEE-754 и может работать с числами двойной точности), а сами вернёмся к рассмотрению разных других строк. С последовательностями цифр мы разобрались. Давайте попробуем добавить какие-нибудь “нецифры”. Перестанет ли строка быть числом? Наверняка вы сами без труда вспомните некоторые случаи, когда этого (может быть) не случится – пробелы в начале и в конце, а также ведущие нули. Действительно, они обрезаются, а оставщаяся строка интерпретируется как число. Итак: 1.2 строка, интерпретируемая как число, также интерпретируется как число, если добавить в начале некоторое количество нулей, при этом ведущие нули игнорируются, 1.3. строка, интерпретируемая как число, также интерпретируется как число, если добавить в начале или в конце некоторое количество пробелов, при этом все пробелы игнорируются. Всё верно? Нет! Во-первых, не забывайте про Максимальное Значение длины, если добавить слишком много нулей или пробелов, строка перестанет быть числом, даже если эти пробелы добавлялись к совершенно безобидному небольшому числу. Во-вторых, добавлять пробелы и нули можно только в строго определённом порядке -- пробелы с краю, нули ближе к "основной части" числа, в другом порядке они уже не будут игнорироваться:
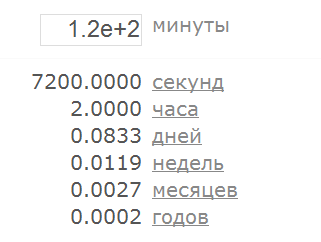
Да, можно эти правила уточнить, ввести понятие “неразрывной последовательности цифр”, к которой уже можно прибавлять пробелы. Но если вы собрались сейчас записать эти правила и повесить на стенку – не делайте этого! Вот вам пример приложения которое действует в точности наоборот – там можно вставлять пробелы куда угодно, хоть в начало, хоть в конец, хоть в середину. А есть и такие (в основном десктопные), в которых пробелы никуда нельзя вставлять, например, так ведёт себя диалог задания размера рисунка в графическом редакторе Paint в Windows 7. Ладно, двигаемся дальше – вспоминаем про отрицательные числа: 1.4. строка, интерпретируемая как число, также интерпретируется как число, если добавить в начало знак минус или плюс. Надеюсь про плюс никто не забыл, да? Кстати, между минусом/плюсом и первой цифрой могут быть пробелы. Ну и перед ними тоже, конечно. Гм… Кажется, у нас проблема. Помните ещё про пустую строку? Мы же согласились считать её как бы числом. Зря согласились – если “перед ней” поставить минус или плюс, числа не получается. Ладно, выкидываем пустую строку, будем рассматривать её отдельно, как особый случай, а минимальную длину последовательности цифр объявим равной единице. Кстати, вас не насторожил тот факт, что я перестал говорить “целое число”? В правиле выделения подобласти 1.1 я его написал, а в следующих правилах нет. Всё верно, эти правила работают также и для нецелых чисел. Добавляем новое правило: 1.5. строка, состоящая из двух неразрывных цепочек цифр, разделённых десятичной точкой, интерпретируется как число Углубляться в подробности, связанные с точностью вычислений не станем, отметим лишь, что здесь тоже можно применить технику разбиения на подобласти. К чему применить? К количеству значащих цифр, или к количеству знаков после запятой, в зависимости от того, как интерпретируется понятие точности в конкретном приложении. Но при этом следует отметить, что для чисел с плавающей точкой техника разбиения на подобласти работает плохо, за подробностями я отправляю вас к статьям Виктора Кулямина про тестирование математических функций (нетерпеливые могут сразу заглянуть в конец раздела 4.3, а любопытные могут поискать ещё другие статьи и презентации на ту же тему на личной страничке Виктора). А всё почему? Потому что JavaScript реализует стандарт IEEE-754. Вообще-то к этому моменту вы, наверное, догадались, что я неспроста уже второй раз упомянул этот стандарт. Да, вы правы. Пришло время перейти к более сложным строкам, которые ну совсем не последовательности цифр, но при этом всё равно интерпретируются как числа. Давайте введём в наше приложение, например, число 120:
Оно работает! Думаете, это только этот конвертер такой, что я специально его выбрал? Ничего подобного! Откройте с десяток наугад выбранных веб-магазинов или онлайн-калькуляторов – добрая половина согласится принять числа в таком формате. А теперь сходите и проверьте своё собственное приложение. Хотя нет, подождите. Это ещё не всё. Во-первых, надо добавить ещё одно правило: 1.6. строка, состоящая из числа, за которым следует символ ‘e’, за которым следует целое число, интерпретируется как число Да, 100e-1 = 10, а плюс можно не указывать, так что 1.0e2 = 1.0e+2 = 100. А во-вторых, есть ещё и другие строки, которые тоже интерпретируются как числа, вот пример:
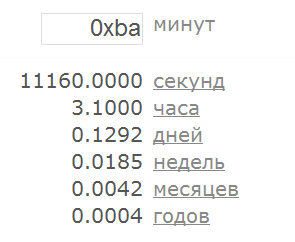
Все числа до этого момента у нас были в десятеричном представлении, а теперь появились шестнадцатеричные. Я намеренно в самом начале, когда ещё первый раз сформулировал правило 1.1 не стал акцентировать внимание на том, что такое “цифра”. Что же, добавляем новое правило: 1.7. строка, состоящая из символов ‘0x’, за которыми следует неразрывная последовательность шестнадцатеричных цифр, интерпретируется как шестнадцатеричное целое число Правило 1.1 при этом придётся тоже уточнить, указав, что там могут участвовать только десятеричные цифры. Приятной новостью является то, что шестнадцатеричные числа могут быть только целые (ну, то есть, в этом приложении так, может быть где-то и дробные бывают). Так что максимум, что можно ещё сделать с ними – добавить плюс/минус, да пробелы в начале и в конце. Ну вот, теперь можете проверять своё приложение, сразу и на числа с плавающей точкой, и на шестнадцатеричные числа. А я тем временем расскажу ещё кое-что про строки, которые могут быть числами. Если ваше приложение написано на языке Pascal или Delphi, думаю, вам будет полезно знать, что в этом языке представляются в несколько ином виде – впереди стоит знак $ (доллар), а не 0x. Однажды мне встретился интернет-магазин, который принимал не только числа в шестнадцатеричном представлении, но и в восьмеричном. То есть ноль в начале не игнорировался, как это бывает обычно, а свидетельствовал о том, что число следует интерпретировать как восьмеричное. Так что правило 1.2 тоже не надо вешать на стенку, и оно не всегда справедливо. Попробуйте в наш подопытный конвертер ввести строку Infinity – вы удивитесь, но это тоже число (а в некоторых языках программирования распознаётся также строка Inf):
В качестве записной книжки для ведения списка дел я использую замечательный сервис Toodledo. Так вот, там при создании записи можно в поле ввода даты написать, например, “tomorrow” или “next Monday” – и оно работает! Для таких преобразований бывают даже специальные библиотеки, например, в языке Perl для анализа дат используется Date::Manip, а для анализа чисел Lingua::EN::Words2Num. Мне лично не приходилось тестировать приложения, где можно было бы вводить числа в текстовом виде, но такое действительно иногда встречается на практике. Ещё одно любопытное “число”, специально для тех, кто знаком с языком программирования Perl – “0 but true”. А вот пример приложения – калькулятор доходности вкладов, в котором число в шестнадцатеричном представлении проходит валидацию, которая выполняется средствами JavaScript, но вызывает проблемы при вычислениях на серверной стороне. Попробуйте указать сумму вклада в шестнадцатеричном виде, например, 0xff – и вы увидите, что серая табличка с расчётами не появится на странице. Добиться аналогичного эффекта, вводя положительные десятеричные числа, мне не удалось. (Примечание: так работал калькулятор во время написания статьи, сейчас реализация уже изменилась) Этот приём позволяет иногда “протолкнуть” через валидатор неправильное значение, которое может привести к сбоям на серверной стороне. В общем, надеюсь, вы поняли, что “строка, которая может быть проинтерпретирована как число” – это не такая простая штука, как может показаться на первый взгляд. А что же попадает во второй большой класс, “нечисла”. Туда попадает всё остальное. Да, вот такое неконструктивное определение. И при этом я обещал в самом начале статьи рассказать вам общую схему рассуждений, позволяющую выполнить разбиение на классы эквивалетности. Пожалуйста, вот эта схема, в одном абзаце: Сначала считаем, что все строки находятся в классе “нечисел”. Как только вы прочитали в требованиях, или в документации, или узнали от коллег, или прочитали в какой-нибудь статье (например, в этой) о том, что строки определённого вида могут интерпретироваться как число – вы выделяете соответствующее подмножество строк и проверяете. Если оказалось, что ваше приложение не считает строки такого вида числами, вы сбрасываете всё обратно в большой класс “нечисел”. Ну а если приложение всё-таки согласилось считать эти строки числами, тогда они выделяются в отдельный подкласс и переводятся в класс “чисел”. Вот и всё, очень простой алгоритм :) Ну так что, принимает ваше приложение шестнадцатеричные числа или нет, а? Обсудить в форуме |